The "Eagle" namespace contains classes that implement vector and geometric algebra as well as interpolation procedures that ultimately allow the construction of camera paths. More...
Namespaces
- namespace PhysicalSpace
Geometric algebra of the physical 3D-space, by which we mean the Clifford algebara over Euclidean, three-dimensional space.
- namespace Plane
Geometric algebra of the plane, by which we mean the Clifford algebra over Euclidean, two-dimensional space.
- namespace STA
Geometric algebra of spacetime, a.k.a.
Classes
- struct AnalyticFunctionBase
- Abstract base class for analytic functions, coordinate-independent. More...
- Abstract base class for analytic functions, coordinate-independent. More...
- class AntiSymmetric
- struct AnyType
- struct Assert< true >
- struct Assertion< true >
- class Assignment
- Convenience class to allow using the comma operator for assigning a sequence of elements to a given array-like class. More...
- Convenience class to allow using the comma operator for assigning a sequence of elements to a given array-like class. More...
- struct BinaryOperatorFunctor
- struct BinaryOperatorNode
- Template node class to perform binary operations on evaluate-able nodes. More...
- Template node class to perform binary operations on evaluate-able nodes. More...
- class BoundingBall
- Bounding container implemented by a ball. More...
- Bounding container implemented by a ball. More...
- class BoundingBox
- class Camera
- Properties of a camera floating around in space, or, alternatively, an eagle's eye. More...
- Properties of a camera floating around in space, or, alternatively, an eagle's eye. More...
- class CameraPath
- struct Cartesian3D
- class Christoffel
- Christoffel symbols. More...
- Christoffel symbols. More...
- class Column
- class ConstantNode
- struct ConstantVectorNode
- class ConstructorNode
- class Context
- struct ContravariantIndexingScheme
- Indices are all upper indices, e.g. More...
- Indices are all upper indices, e.g. More...
- struct CoordinateInfo
- struct CoordinateInfo< void >
- class Coordinates
- Coordinate template class. More...
- Coordinate template class. More...
- struct CovariantIndexingScheme
- Indices are all lower indices, e.g. More...
- Indices are all lower indices, e.g. More...
- struct DegeneratedMatrix
- struct DerivationTrait< BinaryOperatorFunctor< NodeType, NodeType, NodeType, '+'> >
- Computes (u+v),x which is u,x+v,x. More...
- Computes (u+v),x which is u,x+v,x. More...
- struct DerivationTrait< BinaryOperatorFunctor< NodeType, NodeType, NodeType, '-'> >
- Computes (u-v),x which is u,x-v,x. More...
- Computes (u-v),x which is u,x-v,x. More...
- struct DerivationTrait< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '*'> >
- Computes (ab),x which is a,x b + a b,y. More...
- Computes (ab),x which is a,x b + a b,y. More...
- struct DerivationTrait< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '+'> >
- Computes (a+b),x which is a,x+b,y. More...
- Computes (a+b),x which is a,x+b,y. More...
- struct DerivationTrait< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '-'> >
- Computes (a-b),x which is a,x-b,y. More...
- Computes (a-b),x which is a,x-b,y. More...
- struct DerivationTrait< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '/'> >
- Computes (a/b),x which is (a,x b - a b,y) / b^2. More...
- Computes (a/b),x which is (a,x b - a b,y) / b^2. More...
- struct DerivationTrait< LocationComponent< Component > >
- Computes (v[i]),x. More...
- Computes (v[i]),x. More...
- struct DerivationTrait< ScalarCube >
- Computes (y^3),x which is 3 y^2 y,x. More...
- Computes (y^3),x which is 3 y^2 y,x. More...
- struct DerivationTrait< ScalarPlusBivector >
- Computes (a+U),x which is a,x+U,v. More...
- Computes (a+U),x which is a,x+U,v. More...
- struct DerivationTrait< ScalarSquare >
- Computes (y^2),x which is 2 y y,x. More...
- Computes (y^2),x which is 2 y y,x. More...
- struct DerivationTrait< ScalarTimesVector >
- Computes (a*v),x which is a,x * v + a * v,x. More...
- Computes (a*v),x which is a,x * v + a * v,x. More...
- struct DerivationTrait< UnaryMinus< NodeType > >
- Computes (-v),x which is -(v,x) More...
- Computes (-v),x which is -(v,x) More...
- struct DerivationTrait< VectorDotProduct >
- Computes (uv),x which is u,x * v + u * v,x. More...
- Computes (uv),x which is u,x * v + u * v,x. More...
- struct DerivationTrait< VectorSquare >
- Computes (v^2),x which is 2 v v,x. More...
- Computes (v^2),x which is 2 v v,x. More...
- struct DerivationTrait< VectorTimesScalar >
- Computes (a*v),x which is a,x * v + a * v,x. More...
- Computes (a*v),x which is a,x * v + a * v,x. More...
- struct DerivationTrait< VectorWedgeVector >
- Computes
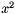 which is
which is 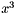 . More...
. More...
- Computes
- struct Determinantor< 1 >
- The trivial determinant of a 1x1 matrix. More...
- The trivial determinant of a 1x1 matrix. More...
- struct Determinantor< 2 >
- The simple determinant of a 2x2 matrix. More...
- The simple determinant of a 2x2 matrix. More...
- struct Determinantor< 3 >
- struct Determinantor< 4 >
- struct ElementOfFunctor
- struct EvaluationContext
- Class providing numerical values from some context ID for the evaluation of function trees. More...
- Class providing numerical values from some context ID for the evaluation of function trees. More...
- class Evaluator
- Abstract base class providing numerical values from some context ID for the evaluation of function trees. More...
- Abstract base class providing numerical values from some context ID for the evaluation of function trees. More...
- struct FA_CONVERT
- class FixedArray
- A FixedArray is a simple copy-by-value array providing random access to its elements. More...
- A FixedArray is a simple copy-by-value array providing random access to its elements. More...
- struct FixedArrayFlattener< FixedArray< FixedArray< T, M >, N > >
- struct FixedArrayFlattener< FixedArray< T, N > >
- struct FixedArrayType
- struct FixedArrayType< ElementType, 1 >
- class GaussSolver
- struct GE
- struct GetFixedArrayType
- struct GT
- class Interpol
- Interpolation of certain values. More...
- Interpolation of certain values. More...
- struct InversionOperation
- struct KDInterface
- class KDTree
- A multidimensional KDTree data structure rewritten from c-code by John Tsiombikas (http://code.google.com/p/kdtree/). More...
- A multidimensional KDTree data structure rewritten from c-code by John Tsiombikas (http://code.google.com/p/kdtree/). More...
- struct KDTreeCallBackFunctor
- struct KDTreeResult< std::list< T > >
- struct KDTreeResult< std::map< double, T > >
- struct KDTreeResult< std::multimap< double, T > >
- struct KDTreeResult< std::vector< T > >
- struct KeyValue
- Entry in interpolation table with some flags. More...
- Entry in interpolation table with some flags. More...
- struct LE
- struct LeibnitzRule
- struct LocationComponent
- Extracts a component of a location. More...
- Extracts a component of a location. More...
- class LowerTriangular
- struct LT
- class Matrix
- Simple matrix class for performing fast operations on matrices of sizes known at compile-time. More...
- Simple matrix class for performing fast operations on matrices of sizes known at compile-time. More...
- struct MetaInfo
- struct MetaInfo< bivector3 >
- struct MetaInfo< Christoffel< N, Scalar_t > >
- struct MetaInfo< Column< N, Scalar_t > >
- struct MetaInfo< Coordinates< Cartesian3D, double >::bivector >
- struct MetaInfo< Coordinates< Cartesian3D, double >::point >
- struct MetaInfo< Coordinates< Cartesian3D, double >::vector >
- struct MetaInfo< FixedArray< T, N > >
- Implement the meta-information on fixed arrays. More...
- Implement the meta-information on fixed arrays. More...
- struct MetaInfo< LowerTriangular< N, Scalar_t > >
- struct MetaInfo< Matrix< R, C, Value > >
- struct MetaInfo< metric33 >
- struct MetaInfo< point3 >
- struct MetaInfo< point3f >
- struct MetaInfo< rgb_t >
- struct MetaInfo< Row< N, Scalar_t > >
- struct MetaInfo< trivector3 >
- struct MetaInfo< tvector3 >
- struct MetaInfo< vector3f >
- struct MetaInfo< Vector< T, N > >
- struct MetaInfo< void >
- struct MetaInfoElementIndex
- For multidimensional types T of rank MetaInfo<T>::RANK, this class provides a mapping from index space to memory space. More...
- For multidimensional types T of rank MetaInfo<T>::RANK, this class provides a mapping from index space to memory space. More...
- struct MetaInfoElementIndex< Christoffel< N, Scalar_t > >
- struct MetaInfoElementIndex< LowerTriangular< N, Scalar_t > >
- struct MetaInfoElementIndex< Matrix< R, C, Value > >
- struct MetaInfoIO
- struct MetaInfoIO< MetaInfo< T > >
- struct MetaInfoNonTensor
- struct MetaInfoNonTensor< Christoffel< N, Scalar_t > >
- class MultiVector
- struct Node
- Abstract base class for evaluation of arbitrary functions that have been parsed from some input. More...
- Abstract base class for evaluation of arbitrary functions that have been parsed from some input. More...
- struct NotElementOfFunctor
- struct OneNode
- struct Operator<'&'>
- struct Operator<'*','~'>
- Multiply with transpose. More...
- Multiply with transpose. More...
- struct Operator<'*'>
- struct Operator<'+','='>
- struct Operator<'+'>
- struct Operator<'-'>
- struct Operator<'/'>
- struct Operator<'='>
- struct Operator<'~'>
- Transpose. More...
- Transpose. More...
- struct OperatorBase
- class ParserContext
- Internal class for communicating with the Bison/Yacc Parser and Flexical Stanza Generator. More...
- Internal class for communicating with the Bison/Yacc Parser and Flexical Stanza Generator. More...
- class Quadratic
- class Row
- struct ScalarCube
- Compute
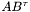 . More...
. More...
- Compute
- struct ScalarPlusBivector
- struct ScalarSquare
- struct ScalarTimesVector
- struct Spherical3D
- class SubMatrix
- class SubQuadratic
- struct SumDerivation
- class Tensor3
- struct TernaryOperatorNode
- Template node class to perform ternary operations on evaluate-able nodes. More...
- Template node class to perform ternary operations on evaluate-able nodes. More...
- class Torsion
- class TransposeOperation
- struct TypedNode
- Base class for evaluation of expressions yielding a specific type, as parsed from some text. More...
- Base class for evaluation of expressions yielding a specific type, as parsed from some text. More...
- struct TypeIndexingScheme
- struct TypeIndexingScheme< bivector3 >
- struct TypeIndexingScheme< metric33 >
- struct TypeIndexingScheme< trivector3 >
- struct TypeIndexingScheme< tvector3 >
- struct TypeIndexingScheme< vector3f >
- struct TypeIndexingScheme< Vector< T, N > >
- struct UnaryMinus
- struct UnaryOperatorNode
- Template node class to perform unary operations on evaluate-able nodes. More...
- Template node class to perform unary operations on evaluate-able nodes. More...
- struct Unit
- http://en.wikipedia.org/wiki/Fundamental_unit In the SI system there are 7 fundamental units: kilogram, meter, candela, second, ampere, kelvin, and mole. More...
- http://en.wikipedia.org/wiki/Fundamental_unit In the SI system there are 7 fundamental units: kilogram, meter, candela, second, ampere, kelvin, and mole. More...
- struct VariableNode
- class Vector
- A Vector is an fixed-size array (see class FixedArray) with vector space operations, i.e. More...
- A Vector is an fixed-size array (see class FixedArray) with vector space operations, i.e. More...
- struct VectorDotProduct
- Dot product between tangential vectors. More...
- Dot product between tangential vectors. More...
- struct VectorizationTrait
- struct VectorSquare
- Computes v^2 for vector v. More...
- Computes v^2 for vector v. More...
- struct VectorTimesScalar
- struct VectorWedgeVector
- class ViewPoints
- struct YlmCoefficients
- struct ZeroNode
Typedefs
- typedef PhysicalSpace::bivector bivector3
- typedef STA::bivector bivector4
- typedef bivector bivector_t
- typedef TypedNode< bivector3 > BivectorNode
- typedef rgba_float_t Color
- typedef unsigned short color16_t
- typedef unsigned char color8_t
-
typedef ConstantNode< ScalarNode > ConstantScalarNode
- A scalar-valued node that yields a constant value, independent from the evaluation context.
- A scalar-valued node that yields a constant value, independent from the evaluation context.
- typedef PhysicalSpace::covector covector3
-
typedef ConstructorNode
< LocationNode > LocationConstructorNode - typedef TypedNode< point3 > LocationNode
- typedef VariableNode< point3 > LocationVariableNode
- typedef PhysicalSpace::Metric metric33
- typedef STA::Metric metric44
- typedef int OperatorID_t
- typedef PhysicalSpace::point point3
-
typedef Coordinates
< Cartesian3D, float >::point point3f - typedef STA::point point4
- typedef Eagle::PhysicalSpace::point point_t
-
typedef Coordinates
< Spherical3D, double >
::Metric polarmetric33 - typedef double pseudoscalar_t
-
typedef Eagle::Vector
< color16_t, 3 > rgb16_t - typedef Eagle::Vector< float, 3 > rgb_float_t
-
typedef Eagle::Vector
< color8_t, 3 > rgb_t -
typedef Eagle::Vector
< color16_t, 4 > rgba16_t - typedef Eagle::Vector< float, 4 > rgba_float_t
-
typedef Eagle::Vector
< color8_t, 4 > rgba_t - typedef PhysicalSpace::rotor rotor3
-
typedef MultiVector
< pseudoscalar_t, MultiVector
< bivector_t, scalar_t > > Rotor4D - typedef TypedNode< rotor3 > RotorNode
- typedef double scalar_t
- typedef TypedNode< double > ScalarNode
- typedef VariableNode< double > ScalarVariableNode
- typedef PhysicalSpace::trivector trivector3
- typedef STA::trivector trivector4
- typedef PhysicalSpace::vector tvector3
- typedef STA::vector tvector4
-
typedef map< string,
Context::id_t > VariableList_t - typedef Plane::vector vector2
-
typedef Coordinates
< Cartesian3D, float >::vector vector3f -
typedef ConstructorNode
< VectorNode > VectorConstructorNode- A node that constructs a vector from three scalar values.
- A node that constructs a vector from three scalar values.
- typedef TypedNode< tvector3 > VectorNode
-
typedef BinaryOperatorFunctor
< VectorNode, VectorNode,
VectorNode, '+'> VectorSumFunctor
-
typedef Operator<'+'> Add
- Addition.
- Addition.
-
typedef Operator<'-'> Sub
- Subtraction.
- Subtraction.
-
typedef Operator<'*'> Mult
- Multiplication.
- Multiplication.
-
typedef Operator<'/'> Div
- Division.
- Division.
-
typedef Operator<'~'> Conj
- Conjugate.
- Conjugate.
-
typedef Operator<','> Deriv
- Derivative.
- Derivative.
-
typedef Operator<'&'> BinaryAnd
- Bit operations.
- Bit operations.
Functions
-
void A_to_lm (int A, int &l, int &m)
- Computation of (l,m) pair from linear index
![\[ l = \sqrt{ A_{lm} } \]](form_33.png)
![\[ m = A_{lm} - l^2 - l \]](form_34.png)
.
- Computation of (l,m) pair from linear index
-
double EAGLE_API abs2_Ylm (int l, int m, double costheta, double phi)
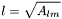 - square of norm of complex spherical harmonic
- square of norm of complex spherical harmonic
- template<int N, class value > void ComputeInverse (Quadratic< N, value > &result, const Quadratic< N, value > &M) throw (DegeneratedMatrix)
- template<class value > void ComputeInverse (Quadratic< 4, value > &B, const Quadratic< 4, value > &A, const value &inv_detA)
- template<class value > void ComputeInverseTimesDetA (Quadratic< 2, value > &result, const Quadratic< 2, value > &M)
- template<class value > void ComputeInverseTimesDetA (Quadratic< 3, value > &result, const Quadratic< 3, value > &M)
- template<class value > void ComputeInverseTimesDetA (Quadratic< 4, value > &result, const Quadratic< 4, value > &M)
-
RefPtr< ScalarNode > cube (const RefPtr< ScalarNode > &x)
- Compute
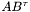 .
.
- Compute
-
template<class value > value Det (const Quadratic< 1, value > &M)
- Determinant of 1x1 matrix (trivial)
- Determinant of 1x1 matrix (trivial)
-
template<class value > value Det (const Quadratic< 2, value > &M)
- Determinant of 2x2 matrix (easy)
- Determinant of 2x2 matrix (easy)
-
template<class value > value Det (const Quadratic< 3, value > &M)
- Determinant of 3x3 matrix (straightforward)
- Determinant of 3x3 matrix (straightforward)
-
template<class value > value Det (const Quadratic< 4, value > &M)
- Determinant of 4x4 matrix (effortsome) http://www.cvl.iis.u-tokyo.ac.jp/~miyazaki/tech/teche23.html.
- Determinant of 4x4 matrix (effortsome) http://www.cvl.iis.u-tokyo.ac.jp/~miyazaki/tech/teche23.html.
- RefPtr< ScalarNode > dot (const RefPtr< VectorNode > &L, const RefPtr< VectorNode > &R)
- bool EagleMatrixCheck ()
- template<int N, class value > void EigenVectorSort (Quadratic< N, value > &V, Row< N, value > &D)
- long double exp (long double x)
- double exp (double x)
- float exp (float x)
-
double faculty (unsigned long n)
- Division of two faculties, i.e. n!/m!
- Division of two faculties, i.e. n!/m!
-
double faculty_div (unsigned long n, unsigned long m)
- Division of two faculties, i.e. n!/m!
- Division of two faculties, i.e. n!/m!
-
double EAGLE_API Im_Ylm (int l, int m, double costheta, double phi)
- Imaginary part of spherical harmonics
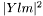 .
.
- Imaginary part of spherical harmonics
- double EAGLE_API Im_Ylm_cc (int l, int m, double costheta, double phi)
- float InnerProduct (float A, float B)
- int InnerProduct (int A, int B)
- double InnerProduct (const double &A, const double &B)
- long double InnerProduct (const long double &A, const long double &B)
- template<int N, class value > value InnerProduct (const Vector< value, N > &A, const Vector< value, N > &B)
-
template<int C, class Value > Column< C, Value > & InterpretAsColumn (Row< C, Value > &A)
- Explicit treatment of a row as column, pure type conversion.
- Explicit treatment of a row as column, pure type conversion.
-
template<int C, class Value > const Column< C, Value > & InterpretAsColumn (const Row< C, Value > &A)
- Explicit treatment of a row as column, pure type conversion, readonly.
- Explicit treatment of a row as column, pure type conversion, readonly.
- template<int C, class Value > Row< C, Value > & InterpretAsRow (Column< C, Value > &A)
- template<int C, class Value > const Row< C, Value > & InterpretAsRow (const Column< C, Value > &A)
-
bool isEqual (double A, double B, double precision=1E-10)
- Compare two doubles with limited precision.
- Compare two doubles with limited precision.
- double Laguerre (int k, double x)
-
int lm_to_A (int l, int m)
- Computation of linear index from (l,m) pair
![\[ A_{lm} = l^2 + l + m \]](form_32.png)
.
- Computation of linear index from (l,m) pair
- long double log (long double x)
- double log (double x)
- float log (float x)
- template<class ResultMatrix , class LeftMatrix , class RightMatrix > void MatrixMultiply (ResultMatrix &result, const LeftMatrix &A, const RightMatrix &B)
- template<class ResultMatrix , class LeftMatrix , class RightMatrix > void MatrixMultiplyTransposed (ResultMatrix &result, const LeftMatrix &A, const RightMatrix &B)
- template<class ResultMatrix , class TransformationMatrix , class DataMatrix > void MatrixTransform (ResultMatrix &result, const TransformationMatrix &A, const DataMatrix &B)
-
int minus_exponential (int m)
- Return
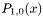 .
.
- Return
- double norm (const PhysicalSpace::tvector &v)
-
double norm (const PhysicalSpace::bivector &v)
- The norm of a bivector.
- The norm of a bivector.
- float norm (float x)
- double norm (double x)
- long double norm (long double x)
- double norm (const PhysicalSpace::Metric &)
-
double norm2 (const PhysicalSpace::tvector &v)
- Compute the squared norm of a vector v, i.e. v.v.
- Compute the squared norm of a vector v, i.e. v.v.
-
double norm2 (const PhysicalSpace::bivector &v)
- Compute the squared norm of a bivector, which is the area spun by the plane.
- Compute the squared norm of a bivector, which is the area spun by the plane.
- float norm2 (float t)
- double norm2 (double t)
- long double norm2 (long double t)
- double norm2 (const PhysicalSpace::Metric &)
- parzival_API RefPtr< Node > One ()
- template<int N, class value > Quadratic< N, value > operator! (const Quadratic< N, value > &M) throw (DegeneratedMatrix)
- parzival_API RefPtr< ScalarNode > operator* (const RefPtr< ScalarNode > &Left, const RefPtr< ScalarNode > &Right)
-
parzival_API MemCore::RefPtr
< VectorNode > operator* (const MemCore::RefPtr< ScalarNode > &, const MemCore::RefPtr< VectorNode > &) - template<int R, int C, class value > Quadratic< R, value > operator* (Matrix< R, C, value > &A, Matrix< C, R, value > &B)
-
template<int C, class Value > Row< C, Value > operator* (const Row< C, Value > &A, const double &V)
- Multiply row vector by double.
- Multiply row vector by double.
-
template<int C, class Value > Column< C, Value > operator* (const Column< C, Value > &A, double V)
- Multiply column vector by double.
- Multiply column vector by double.
- template<int N, class Value > Value operator* (const Row< N, Value > &l, const Column< N, Value > &r)
- parzival_API RefPtr< ScalarNode > operator+ (const RefPtr< ScalarNode > &Left, const RefPtr< ScalarNode > &Right)
-
parzival_API MemCore::RefPtr
< VectorNode > operator+ (const MemCore::RefPtr< VectorNode > &, const MemCore::RefPtr< VectorNode > &) - parzival_API RefPtr< ScalarNode > operator- (const RefPtr< ScalarNode > &Left, const RefPtr< ScalarNode > &Right)
-
parzival_API MemCore::RefPtr
< VectorNode > operator- (const MemCore::RefPtr< VectorNode > &, const MemCore::RefPtr< VectorNode > &) - template<class NodeType > MemCore::RefPtr< NodeType > operator- (const MemCore::RefPtr< NodeType > &V)
- template<class Domain , class real > Coordinates< Domain, real >::vector operator- (const typename Coordinates< Domain, real >::point &a, const typename Coordinates< Domain, real >::point &b)
- parzival_API RefPtr< ScalarNode > operator/ (const RefPtr< ScalarNode > &Left, const RefPtr< ScalarNode > &Right)
-
parzival_API MemCore::RefPtr
< BivectorNode > operator^ (const MemCore::RefPtr< VectorNode > &, const MemCore::RefPtr< VectorNode > &)- Wedge product of two 3-vectors, yielding a bivector.
- Wedge product of two 3-vectors, yielding a bivector.
- RefPtr< BivectorNode > operator^ (const RefPtr< VectorNode > &L, const RefPtr< VectorNode > &R)
-
template<int N, class value > Quadratic< N, value > operator~ (Quadratic< N, value > Q)
- Return the transposed n x n square matrix.
- Return the transposed n x n square matrix.
- bool overlap (const BoundingBall &A, const BoundingBall &B)
- double P2 (double x)
- double P3 (double x)
- double P4 (double x)
- double P5 (double x)
- double P6 (double x)
-
double EAGLE_API Re_Ylm (int l, int m, double costheta, double phi)
- Real part of spherical harmonics
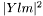 .
.
- Real part of spherical harmonics
- double EAGLE_API Re_Ylm_cc (int l, int m, double costheta, double phi)
- template<class ResultType > MemCore::RefPtr< typename
ResultType::TypedNode_t > * RefNode (ResultType *N) - rgb_t rgb2bgr (const rgb_t &bgr)
- rgb_t rgb2bgr (const unsigned char bgr[3])
- template<typename T > T sinc (T x)
- template<int N, class value > void SortedEigenVectors (LowerTriangular< N, value > &A, Quadratic< N, value > &RRmatrix, Row< N, value > &E, double precision=1E-10)
- void speak (const RefPtr< BoundingBox > &BBox, const char *context)
- aerie_API void speak (const MemCore::RefPtr< BoundingBox > &BBox, const char *context="")
- double sqr (double x)
-
RefPtr< ScalarNode > square (const RefPtr< ScalarNode > &x)
- Compute
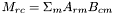 .
.
- Compute
- template<class T , int N> Vector< T, N > & Vector_cast (FixedArray< T, N > &F)
- template<class T , int N> const Vector< T, N > & Vector_cast (const FixedArray< T, N > &F)
- double Y_factor (int l, int m)
- double Y_normalization (int l, int m)
-
std::complex< double > EAGLE_API Ylm (int l, int m, double costheta, double phi)
- Spherical harmonics, complex return value.
- Spherical harmonics, complex return value.
- template<class Coefficients > std::complex< double > Ylm (double theta, double phi, const Coefficients &A, int L, int K)
-
std::complex< double > EAGLE_API Ylm_sincos (int l, int m, double costheta, double sin_mphi, double cos_mphi)
- Spherical harmonics, complex return value with precomputed
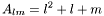 .
.
- Spherical harmonics, complex return value with precomputed
- parzival_API RefPtr< Node > Zero ()
- parzival_API RefPtr< Node > ZeroOrOne (bool One)
-
double P0 (double x)
-
double P1 (double x)
-
double Pn (int n, double x)
-
double Plm (int l, int m, double x)
Variables
- parzival_API template class BinaryOperatorNode< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '*'> >
- parzival_API template class BinaryOperatorNode< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '+'> >
- parzival_API template class BinaryOperatorNode< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '-'> >
- parzival_API template class BinaryOperatorNode< BinaryOperatorFunctor< ScalarNode, ScalarNode, ScalarNode, '/'> >
- parzival_API template class BinaryOperatorNode< BinaryOperatorFunctor< VectorNode, VectorNode, VectorNode, '-'> >
- parzival_API template class BinaryOperatorNode< VectorSumFunctor >
- const rgba_float_t BLACK = makeColor(0, 0, 0, 1)
- const rgba_float_t BLUE = makeColor(0, 0, 1, 1)
- parzival_API template class ConstantNode< ScalarNode >
- const rgba_float_t CYAN = makeColor(0, 1, 1, 1)
- const rgba_float_t DARKGREY = makeColor(.25, .25, .25, 1)
- const rgba_float_t GREEN = makeColor(0, 1, 0, 1)
- const rgba_float_t GREY = makeColor(.5, .5, .5, 1)
- const rgba_float_t LIGHTGREY = makeColor(.75, .75, .75, 1)
- const rgba_float_t MAGENTA = makeColor(1, 0, 1, 1)
- struct parzival_API OneNode
- const rgba_float_t RED = rgba_float_t(1, 0, 0, 1)
- parzival_API template class TernaryOperatorNode< ElementOfFunctor< GE, LE > >
- parzival_API template class TernaryOperatorNode< NotElementOfFunctor< LT, GT > >
- parzival_API template class TypedNode< double >
- parzival_API template class UnaryOperatorNode< LocationComponent< 0 > >
- parzival_API template class UnaryOperatorNode< LocationComponent< 1 > >
- parzival_API template class UnaryOperatorNode< LocationComponent< 2 > >
- struct parzival_API VariableNode
- const rgba_float_t WHITE = makeColor(1, 1, 1, 1)
- const rgba_float_t YELLOW = makeColor(1, 1, 0, 1)
- struct parzival_API ZeroNode
Detailed Description
The "Eagle" namespace contains classes that implement vector and geometric algebra as well as interpolation procedures that ultimately allow the construction of camera paths.
The naming of the namespace is inspired by the sharp eye of the eagle, that requires description by the mathematics of geometric algebra. A camera path's purpose is a smooth flight through a virtual scene, like an eagle smoothly flies through a real scene.
Typedef Documentation
| typedef int Eagle::OperatorID_t |
The type identifying an Operator.
See class Operator for usage.
| typedef TypedNode<double> Eagle::ScalarNode |
Base class for evaluation of a scalar function that has been parsed from some input.
RefPtr<ScalarNode> MyNode = ...;
EvaluationContext EV;
double value = MyNode->eval(EV);
| typedef TypedNode<tvector3> Eagle::VectorNode |
Base class for evaluation of a vector-valued function that has been parsed from some input.
using namespace Eagle; RefPtr<VectorNode> MyNode = ...; EvaluationContext EV; PhysicalSpace::tvector value = MyNode->eval(EV);
Function Documentation
| double Eagle::norm | ( | const PhysicalSpace::tvector & | v | ) | [inline] |
Compute the Euclidan norm of a vector.
Note that if just the square of the norm is required, then function norm2() is more efficient since the square root does not need to be taken.
| Value Eagle::operator* | ( | const Row< N, Value > & | l, |
| const Column< N, Value > & | r | ||
| ) | [inline] |
Contraction operation: multiply row by column.
Note that the reverse operation, ie. multiplying a column by a row, is the tensor product and yields a $n n$ matrix.
| MemCore::RefPtr<typename ResultType::TypedNode_t>* Eagle::RefNode | ( | ResultType * | N | ) |
ingroup parzival Create a new reference pointer appropriate for the class given.
This is a convenience function for the Quest parser, since that one can only deal with native C pointers in the main union data type. It is not supposed to be used anywhere else than in this specific context.
| T Eagle::sinc | ( | T | x | ) | [inline] |
The sinc(x) function, save for x=0, and numerically stable around x=0.
When the sine function is written as a taylor series,
![\[ sin(x) = x - x^3/3! + x^5/5! - x^7/7! \]](form_22.png)
we get the sinc(x) function as
![\[ sin(x)/x = 1 - x^2/(2*3) + x^4/(2*3*4*5) - \cdots = 1 - x^2 [ 1 - x^2 / 20 ] / 6 \]](form_23.png)
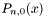
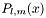
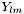
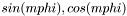
 1.7.5
1.7.5