A rotor is the sum of scalar with a bivector. More...
#include </home/werner/origo/vish/ocean/eagle/rotor3.hpp>
Public Member Functions
-
bivector & bivec ()
- Retrieve bivector component, read-only.
- Retrieve bivector component, read-only.
-
const bivector & bivec () const
- Retrieve bivector component, read-only.
- Retrieve bivector component, read-only.
-
rotor conj () const
- Compute the conjugate rotor.
- Compute the conjugate rotor.
- double degrees () const
-
rotor inv () const
- Compute the inverse rotor.
- Compute the inverse rotor.
- vector operator() (const vector &v) const
-
bivector operator() (const bivector &V) const
- Rotate a bivector.
- Rotate a bivector.
-
OddMultiVector operator* () const
- Applying the hodge star operator.
- Applying the hodge star operator.
- rotor operator+ (const rotor &r)
- double radians () const
-
rotor (const Vector< double, 4 > &V)
- Explicit construction from double's.
- Explicit construction from double's.
-
rotor (double r, const bivector &b)
- Construct rotor from scalar and bivector.
- Construct rotor from scalar and bivector.
-
rotor (const bivector &b, double r)
- Construct rotor from bivector and scalar.
- Construct rotor from bivector and scalar.
-
rotor ()
- Default constructor.
- Default constructor.
-
rotor (const rotor &b)
- Copy constructor.
- Copy constructor.
-
rotor (const double s)
- Create rotor with just scalar component, bivector is zero.
- Create rotor with just scalar component, bivector is zero.
-
rotor (const rotor &b, const Operator<'~'> &)
- Computational constructor computing the conjugate (inverse) rotor.
- Computational constructor computing the conjugate (inverse) rotor.
-
double & scalar ()
- Retrieve scalar component, modifyable.
- Retrieve scalar component, modifyable.
-
double scalar () const
- Retrieve scalar component, read-only.
- Retrieve scalar component, read-only.
-
rotor unit () const
- Normalize to a unit rotor (added by mr).
- Normalize to a unit rotor (added by mr).
Friends
- double norm2 (const rotor &r)
- rotor operator* (const rotor &, double)
- rotor operator* (double, const rotor &)
-
rotor operator* (const rotor &, const rotor &)
- Multiply rotors, which is a concatenation operation of rotations.
- Multiply rotors, which is a concatenation operation of rotations.
- rotor operator* (const rotor &, const vector &)
-
vector & operator*= (vector &v, const rotor &R)
- Rotate a certain vector by a rotor "in place".
- Rotate a certain vector by a rotor "in place".
- bivector & operator*= (bivector &V, const rotor &R)
- rotor operator/ (const rotor &, double)
- std::ostream & operator<< (std::ostream &os, const rotor &r)
Related Functions
(Note that these are not member functions.)
- rotor exp (const bivector &U, double phi)
- rotor exp (const bivector &i)
- vector operator% (const vector &l, const vector &r)
- bivector operator() (const bivector &V) const
- rotor operator* (const vector &l, const vector &r)
-
rotor operator+ (double r, const bivector &U)
- Create a rotor as sum of scalar and bi-vector.
- Create a rotor as sum of scalar and bi-vector.
-
rotor operator+ (const bivector &U, double r)
- Create a rotor as sum of bi-vector and scalar.
- Create a rotor as sum of bi-vector and scalar.
-
rotor operator+ (double r, const rotor &U)
- Add a scalar value to a rotor.
- Add a scalar value to a rotor.
-
rotor operator+ (const rotor &U, double r)
- Add a scalar value to a rotor.
- Add a scalar value to a rotor.
- rotor operator/ (const rotor &l, const rotor &r)
- rotor operator/ (const vector &l, const vector &r)
- rotor operator~ (const rotor &r)
- rotor pow (const rotor &r, double t)
- Matrix< 4, 4, double > rotmatrix (const rotor &r)
- rotor slerp (const rotor &q1, double t, const rotor &q2)
Detailed Description
A rotor is the sum of scalar with a bivector.
It represents the even subalgebra (for instance grade 0 and 2) of the geometric algebra of euclidean 3-space and implements the same algebraic properties as a Pauli spinor. There are 3+1 components in a rotor in 3-space.
To use a rotor to rotate a vector v around a bivector u look at rotor::operator()
- Todo:
- Need to implement optimization for unit rotors, such that the norm2() function always returns 1.0 without computation.
Member Function Documentation
Compute Rv ~R, which is the rotation of the vector v along the current vector R.
R(v) = R v ~R = (s+U) v (s-U) = (s v + U v) (s-U) = s v s + U v s - s v U - U v U = s s v + Uv s - s vU - U(v) = ss v + 2 Uv s - U(v)
To rotate a vector v with angle phi around a bivector u you may use:
bivector u;
vector v;
double phi;
roto R = exp(u * phi); // with ||u||=1 (use unit() ) and [phi] in rad
vector rotated_v = R(v);
- Todo:
- Hmm, isn't there a sign error in the 2 s vU part? Plz verify!!
Friends And Related Function Documentation
Implement a rotation of phi degrees along the bivector U. If U is not unit, then the resulting rotor will also scale a given vector.
- Parameters:
-
phi Rotation in radians.
Compute the exponential of a bivector, which implements a rotation as given by the norm of the bivector.
Compute the three-dimensional cross product
| bool Wizt::lessValueSetPtr::operator() | ( | const bivector & | V | ) | const [related] |
Rotate a bivector. This operator is equivalent to 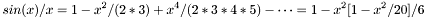 .
.
- Note:
- Let's hope the compiler optimizes this function sufficiently.
The multiplication operation on two vectors implements the geometric product  , thus generating a clifford algebra.
, thus generating a clifford algebra.
Geometrically it means the operation to sweep one vector r to a vector l, which results in a rotor.
Rotate a certain bivector by a rotor "in place".
- Note:
- This is numerically not more efficient than assignment.
Divide two vectors, yielding the rotation operation to sweep the second vector to the first one (or vice versa, I forgot :) ).
Compute the inverse rotor.
- Note:
- This is probably only correct for unit rotors...
Compute the classical 4x4 rotation Matrix. E.g. for use with openGls: glMultMatrixd like: glMultMatrixd( RotMat.ptr() );
Interpolate between q1 (t = 0) and q2 (t = 1): q = (q2/q1)^t q1 .
The documentation for this class was generated from the following files:
- ocean/eagle/rotor3.hpp
- ocean/eagle/STA.hpp
- ocean/plankton/ValueSet.cpp
 1.7.5
1.7.5