Quadratic< N, Value > Class Template Reference [Small Matrix Classes]

An n x n matrix (i.e., a vector of length n*n), stored row-wise: that is, A(i,j) = A[ij], where ij = i*n + j. More...

#include <ocean/eagle/QuadraticMatrix.hpp>

Inheritance diagram for Quadratic< N, Value >:

List of all members.

Public Types

• typedef Matrix< N, N, Value > Base_t
• typedef FixedArray< int, N > PermutationVector_t

  Type of the permutation vector that is required for the functions GaussDecompose() and GaussSolve().
  

• typedef Value value_type

Public Member Functions

• bool GaussDecompose (FixedArray< int, N > &perm, double EPSWEIGHT=1E-3)

  Perform gauss decomposition of the matrix, which can and should be used instead of computing the inverse of a matrix.
  

• void GaussSolve (const PermutationVector_t &perm, const Column< N, value > &b, Column< N, value > &x) const

  Instead of inverting a matrix, solve a linear system of equations by forward and backward elimination.
  

• value maxoffd () const

  Return maximum off-diagonal element of n by n square matrix A.
  

• template<class OutputValue > LowerTriangular< N, OutputValue > operator() (const LowerTriangular< N, OutputValue > &A) const
• template<class OutputValue > Quadratic< N, OutputValue > operator() (const Quadratic< N, OutputValue > &A) const
• Quadratic & operator= (const LowerTriangular< N, value > &)
• Quadratic (const LowerTriangular< N, value > &)

  Construct a quadratic matrix from a lower triangular matrix.
  

• Quadratic (Quadratic &, const TransposeOperation &)
• template<int C, class ValueA , class ValueB > Quadratic (const Matrix< N, C, ValueA > &A, const Matrix< C, N, ValueB > &B)

  Construct quadratic matrix from multiplication for two fitting non-quadratic matrices.
  

• Quadratic (const Matrix< N, N, value > &A)

  Construct quadratic matrix from base class.
  

• Quadratic ()

  Default constructor.
  

---

Detailed Description

template<int N, class Value>
class Quadratic< N, Value >

An n x n matrix (i.e., a vector of length n*n), stored row-wise: that is, A(i,j) = A[ij], where ij = i*n + j.

See also:

Matrix

Examples:

Matrix.cpp.

---

Member Function Documentation

template<int N, class Value>

bool Quadratic< N, Value >::GaussDecompose	(	FixedArray< int, N > &	perm,
		double	EPSWEIGHT = 1E-3
	)			[inline]

Perform gauss decomposition of the matrix, which can and should be used instead of computing the inverse of a matrix.

The permutation operations during the composition is stored in the perm parameter, which then needs to be provided to the GaussSolve() routine.

Author:

Marcus Weber, ZIB, based on "Formelsammlung zur Numerischen Mathematik mit C-Programmen" von G.Engeln-Maellges und F.Reutter"

Note:

The original matrix is destroyed during this operation.

Parameters:

EPSWEIGHT

square root of the absolut precision of the computation

template<int N, class Value>

void Quadratic< N, Value >::GaussSolve	(	const PermutationVector_t &	perm,
		const Column< N, value > &	b,
		Column< N, value > &	x
	)			const [inline]

Instead of inverting a matrix, solve a linear system of equations 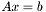by forward and backward elimination.

Parameters:

	perm	A permutation vector as computed by GaussDecompose()
	b	The right-hand side of the equation
	x	On return, will contain the solution.

        Eagle::Quadratic<3, double> A;
        Eagle::Column<3, double> b;
        Eagle::Column<3, double> x;
        Eagle::FixedArray<int, 3> perm;

        A = 2.5,  3.0, 1.1,
            0.2,  0.1, 2.1,
            0.12, 1.0, 0.3;

        b = 39.0, 1.0, 34.33;

        A.GaussDecompose(perm);
        A.GaussSolve(perm, b, x);

The result in x then is < 16.809817, -24.730900, 16.013638 >.

---

The documentation for this class was generated from the following file:

• ocean/eagle/QuadraticMatrix.hpp