Public Types | Public Member Functions | Public Attributes

Interpolate< N, Type, Interpol, CoordinateType, Delimiter, DerivativeDimension > Struct Template Reference

Recursive multidimensional interpolator of arbitrary degree. More...

#include <Interpolate.hpp>

List of all members.

Public Types

Public Member Functions

Public Attributes

Detailed Description

template<int N, class Type, class Interpol, class CoordinateType, class Delimiter, int DerivativeDimension>
struct Interpolate< N, Type, Interpol, CoordinateType, Delimiter, DerivativeDimension >

Recursive multidimensional interpolator of arbitrary degree.

The purpose of this class is to push the definition of a one-dimensional interpolator, defined in the `Interpol' argument, to a n-dimensional regular grid in a recursive manner.

The interpolator is initialized with a reference to a interpolation point and a multidimensional array. The interpolated value is retrieved through the eval() function. For subsequent interpolation requests, the references interpolation point may be modified and the eval() function called again: 

 MultiArray<3, double> Data;
 FixedArray<3, double> point;

 Interpolate<3, double, LinearIpol<double> > DataField(Data, point);

        point = 5.5, 6.7, 8.8;
 double value = DataField.eval();
 
        point = 2.3, 4.5, 9.2;
        value = DataField.eval();

At the same time, an Interpolator<> class instance looks like a one-dimensional vector<>, i.e. it provides the [] operator and a size() member function. Calling these functions allows to traverse an interpolated one-dimensional line which has its coordinates fixed to those of the current interpolation point.

Parameters:
DerivativeDimension The interpolator may also compute the derivative by the nth coordinate during interpolation. This parameter specifies the coordinate for which the derivation should be performed. It is straightforward to compute the derivative during interpolation since then derivative of the interpolation formulas can be employed. The derivative dimension is a compile-time parameter because the resulting Interpolate object is intended to conform to the concept of an array, i.e. it shall provide an [] operator which is indiced with a single index only. There is no way to specify another parameter through this interface. As this parameter is required only locally within operator[], technically it were also possible to provide the derivative dimension as a runtime parameter (e.g. as a member variable or a different interface), if the actual reason indeed arises somewhen. For usual interpolation with no derivative, set this parameter to a negative value.
Delimiter An object that is forwarded to the one-dimensional interpolator from the uppermost level. Its layout is not used by the Interpolate class, but the one-dimensional interpolators may use it to e.g. perform local alignment of eigenvector fields on all interpolation vertices. With no special needs, class NoDelimiter<Type> may be used here.
Interpol A one-dimensional interpolator type. Currently implemented one-dimensional interpolators are

  1. NearestNeighborIpol (fastest, but nothing really precise)
  2. LinearIpol (speedy, providing fair results)
  3. FastCubicIpol (nearly same speed as LinearIpol, but with smooth derivatives)
  4. CubicIpol (slower than linear, but very accurate)
  5. CatMullRomSpline (advanced, but apparently same as cubic, little slower)
CoordinateType Explicit specification on which coordinates are to be used for interpolation. This type is used for storing the local point of interest, which is actually a reference to an external variable. There is not much need to specify something else than float or double here. In conjunction with the dimensionality parameter N it defines the coordinates on the underlying manifold. The actual interpolation type is then of type FixedArray<N,CoordinateType>.
N The dimensionality of the underlying manifold. This interpolator is good for MultiArrays of same dimension.
Type The type of the field defined on each element of a MultiArray to be interpolated. The result of the interpolation will be of same type. Note that this type does not need to be the same as the value type of the Storage: It may be double, whereas the Storage contains unsigned char's, thereby yielding interpolated doubles from unsigned char values (which is of course more precise).
Examples:

InterpolatedDerivative.cpp, InterpolatedVectorDerivative.cpp, and Interpolation.cpp.

Constructor & Destructor Documentation

template<int N, class Type, class Interpol, class CoordinateType, class Delimiter, int DerivativeDimension>
Interpolate< N, Type, Interpol, CoordinateType, Delimiter, DerivativeDimension >::Interpolate ( const MultiArray_t &  m,
const Point_t &  point 
) [inline]

Basic constructor.

Parameters:
m The multidimensional array which provides the data for a multidimensional index.
point The fractional index location where the data value is to be computed.
template<int N, class Type, class Interpol, class CoordinateType, class Delimiter, int DerivativeDimension>
Interpolate< N, Type, Interpol, CoordinateType, Delimiter, DerivativeDimension >::Interpolate ( const MultiArray_t &  m,
const Eagle::VVector< N, CoordinateType > &  point 
) [inline]

Convenience constructor which takes a vvectorized coordinate point.

Parameters:
m The multidimensional array which provides the data for a multidimensional index.
point The fractional index location where the data value is to be computed.

Member Function Documentation

template<int N, class Type, class Interpol, class CoordinateType, class Delimiter, int DerivativeDimension>
Type Interpolate< N, Type, Interpol, CoordinateType, Delimiter, DerivativeDimension >::operator[] ( index_t  i  )  const [inline]

Perform an interpolation along the 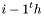${i-1}^th$ dimension, i.e.

the highest dimension of the interpolation point is ignored.

References MultiArrayBase< N, T >::Size().

Generated on Wed Jan 26 07:24:35 2011 for FiberVISH by  doxygen 1.6.2